This is an edition of Quintessence, a series about fundamental ideas in science.
The pigtailed macaque often get into petty fights. However, if more than five monkeys start a fight, it escalates to an all out brawl. Scientists have observed a similarly abrupt behavioural transition in Anelosimus studiosus, a species of spider. Colonies of these spiders generally coexist peacefully, but when the ambient temperature climbs past 31º C, violence ensues.
In both stories, dramatic changes happen when some parameter crosses a critical threshold. Such thresholds are commonly called tipping points, a term popularised by Malcolm Gladwell’s book of the same name. However, Gladwell defined qualitative tipping points for social contexts whereas the concept was already commonplace in the toolboxes of physicists and mathematicians.
Tipping points show up not just in animal societies but in many ecological scenarios as well. For example, scientists have known of vast patches of land that desertified abruptly due to gradual changes in the environment, or of lakes turning turbid in no time due to changes in their nutrient uptake. These are complex systems responding to numerous environmental and societal cues. Keeping track of all these cues and the responses they elicit is often impossible, so scientists have turned to techniques that can simplify these interactions.
One way is to transform these physical systems into a collection of mathematical equations. Different terms in these equations account for different details. Scientists call this approach reduced order modelling. Apart from making notoriously difficult problems open to analysis, this method allows researchers to invoke nonlinear dynamics, a branch of physics and mathematics.

Scientists use nonlinear dynamics to track how a system responds when it is prodded by an external disturbance. If a swinging pendulum is jolted slightly off course, physicists have a set of equations informed by the principles of nonlinear dynamics to calculate its new path.
When tipping points began to appear in ecology, biology, etc., scientists began to appeal to work mathematicians had already done to study similarly abrupt transitions. Specifically, the scientists were curious if they could use these techniques, together with reduced order modelling, to help them make sense of why some systems tip over from one state to another.
Let us reduce the behaviour of a colony of heat-stressed Anelosimus studiosus spiders into a set of equations and process them with nonlinear dynamics. The process spits out a three-dimensional graph that looks like it has mountains and valleys.
This graph is the landscape. Each feature on the landscape stands in for a state of the system. In our example, these states are ‘cooperative’ and ‘aggressive’. The system is said to be stable if it is at the bottom of a valley: like a ball dropped there, it can’t climb out of the valley to a new state unless it is supplied the energy to do so. However, a system at the top of a mountain is very unstable: like a ball, it can roll down in one of any number of directions at the slightest touch.
So say we start out at 21º C, and the system is in a stable ‘cooperative’ valley, separated from the ‘aggressive’ state valley by a small mound. There are two ways for the system to go from one valley to the other: either the external disturbances are strong enough to get the system over the mound or something makes the mound itself go away.
When scientists increased the temperature, they found the mound became smaller and smaller until, at just below 31º C, the two states were separated by flat land. This is the tipping point. Any further erosion could cause the ‘cooperative’ state to be higher than the ‘aggressive’ state, and the system would roll down to its macabre destiny.
Using the visuals of mountains and valleys, and a ball rolling across them, also throws up other interesting insights into the idea of tipping points.
For example, as long as the mound stood (to whatever height), the system lazed in the stable valley, oblivious to the perils on the other side. But when the mound disappeared, the system was suddenly faced with a drastic transition.
For another, even if the mound hadn’t been flattened all the way and remained as a small lump on the landscape, it could cause the valley behind it – the ‘cooperative’ valley – to become shallower (see image below). A system at the bottom of a shallower valley takes longer to settle down after a nudge than a system in a deeper one, just like a ball might spend longer to come to rest at the bottom of a bowl than it would in a drum.
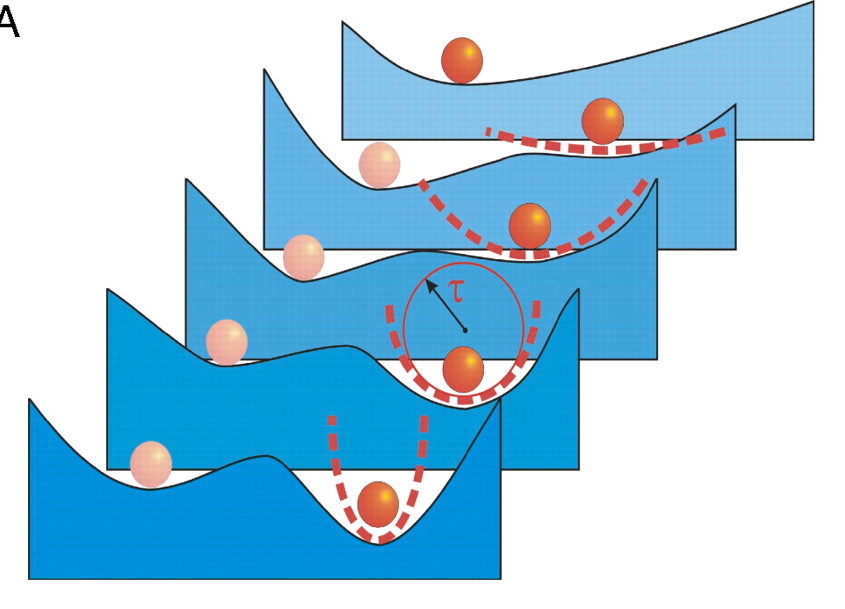
A schematic showing how the stability landscape changes when the mound between two valleys is eroded. The time of recovery from perturbation becomes longer as the valley becomes flatter. Image: 10.1073/pnas.0705414105
This behaviour is a giveaway that the system is ‘dissatisfied’ with its current state and is probably going to tip into another one. Researchers use it to identify systems moving towards tipping points, like bacterial communities at the cusp of extinction or, as it happens, our planet itself.
One of the most complex systems we know of is Earth’s climate. It is a mostly intractable beast of many moving parts interacting in ways we don’t fully understand. Climatologists have identified many potential tipping points in this system, most of which have to do with the natural processes, or engines, that drive heat and water circulation. Even if only one of these engines fails, the system could change catastrophically.
The climate also has many positive feedback loops – processes that, when disturbed, amplify the disturbance. For example, ice reflects heat, so when global heating melts ice, less heat is sent back to space and more lingers on Earth’s surface. This in turn causes even more ice to melt. This way, these loops can reinforce otherwise innocuous perturbations and cause a system to tip over to a new state.
So Earth has two paths in front of it: either its environment gets bad because we have disturbed it so much and positive feedback loops make it worse – or climate change alters the planet’s stability landscape and creates tipping points that, in turn, bring on catastrophic changes. Both paths lead to new states, and both states promise to be hellscapes.
Also read: What Is Quantum Biology?
In fact, the idea of tipping points has come to dominate climate science. The term is often used in a more general sense to invoke a sense of immediacy, even if how close we are to bypassing one or more such points is the subject of furious debate. This is primarily because it is so difficult to obtain quantitative measurements of the climate’s stability and resilience. Even the best climate models struggle to predict and capture abrupt changes.
If someone asks you if we are actually near any tipping points or if we have we already crossed one, the correct answer is that we don’t know for sure. What we do know is that humans have radically changed the stability landscape of Earth’s climate, making it more cryptic and potentially even causing a runoff calamity.
In this time, history won’t guide us because there have been no precedents for such change. That said, prevailing wisdom suggests that we should be able to guide Earth away from this dangerous path by building an alternate one. In other words, we need to resculpt the stability landscape. It would no doubt require a global collaboration of the kind we haven’t had before, but today is all about doing things for the first time.
Note: The article originally stated that Anelosimus studiosus spiders become cannibalistic when the ambient temperature crosses 31º C. They don’t; they become more violent. The mistake was corrected at 11:54 am on August 7, 2019.
Ronak Gupta is doing a PhD in fluid mechanics at the University of British Columbia, Vancouver.
